Bokun Wang
Postdoctoral Researcher at UT Austin
I am a Postdoctoral Fellow in the Department of Electrical and Computer Engineering (ECE) at The University of Texas at Austin, working with Prof. Diana Marculescu and the EnyAC group. Before that, I received my Ph.D. degree in Computer Science at Texas A&M University, advised by Prof. Tianbao Yang.
My research interest lies in Efficient Generative AI (Memory | Compute | Data).
Email: bokun.wang@utexas.edu
Research
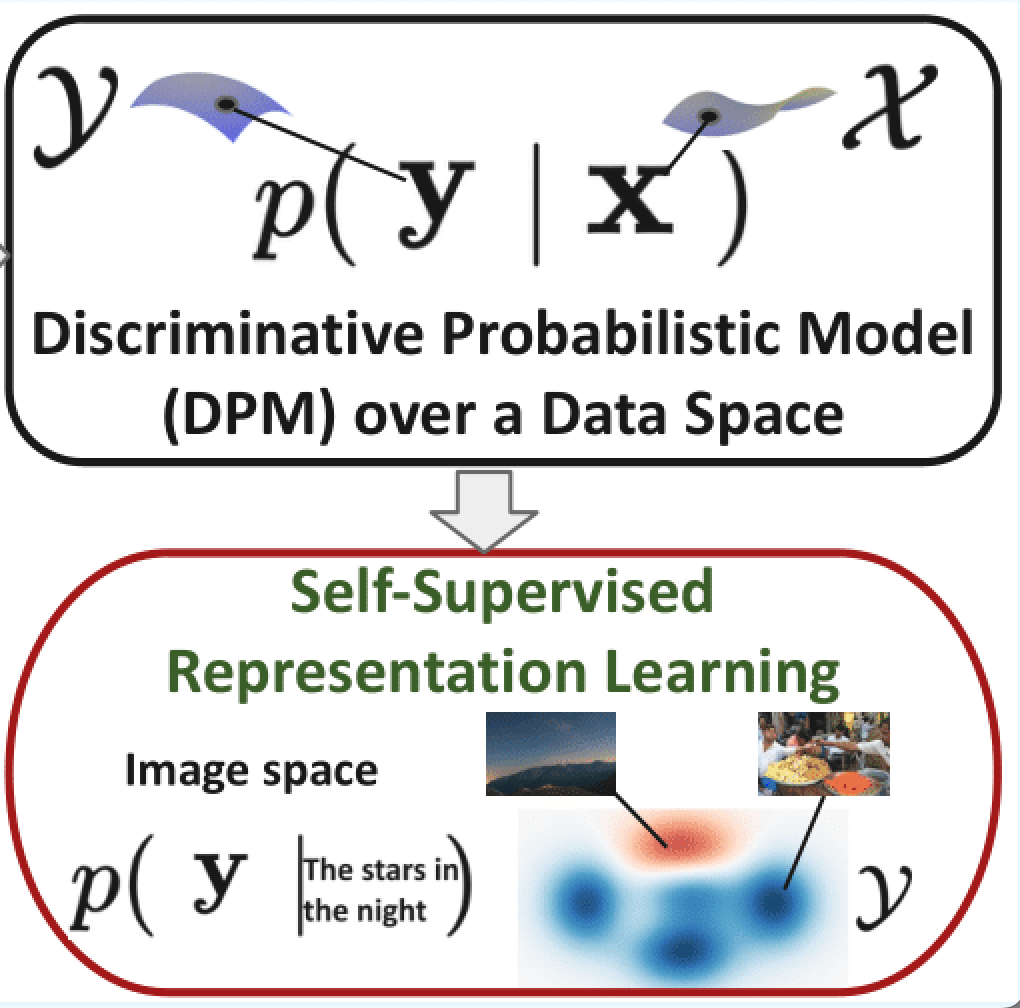
Theory-driven Efficient Algorithms for SSL
This project focuses on developing efficient algorithms for (multi-modal) self-supervised representation learning (SSL) with convergence and generalization guarantees.
Recent Publications (Full List)
Teaching
- Guest Lecturer, CSCE 689: Optimization for Machine Learning (Fall 2023), Texas A&M University.
- Teaching Assistant, ECS 32B: Introduction to Data Structures (Winter 2020), University of California Davis.
- Teaching Assistant, ECS 154A: Computer Architecture (Fall 2019), University of California Davis.
- Teaching Assistant, ECS 170: Introduction to Artificial Intelligence (Spring 2019), University of California Davis.
- Teaching Assistant, ECS 271: Machine Learning and Data Discovery (Winter 2019), University of California Davis.